一、背景
AC自动机以Trie树为基础的,每一个状态都由一个TrieNode来表示,TireNode的定义如下:
1 | struct TrieNode { |
测试过程中29W个关键词来构建出的Trie树有762922个TrieNode节点,每个节点占用内存空间20byte,则占用内存空间为
1 | 762922 * 20 / 1024 / 1024 = 46M |
仅仅是TireNode节点占用的空间已经达到了46M,加上额外keyword和map指向的内存占用,会直接达到100M左右,显然在内存受限的场景中是无法接受的。
因此基于双数组Tire树的AC自动机被提出,以降低AC自动机的内存占用。
二、双数组Tire树介绍
双数组Trie (Double-Array Trie)结构由日本人JUN-ICHI AOE于1989年提出的,是Trie结构的压缩形式,仅用两个线性数组来表示Trie树,该结构有效结合了数字搜索树(Digital Search Tree)检索时间高效的特点和链式表示的Trie空间结构紧凑的特点。双数组Trie的本质是一个确定有限状态自动机(DFA),每个节点代表自动机的一个状态,根据变量不同,进行状态转移,当到达结束状态或无法转移时,完成一次查询操作。在双数组所有键中包含的字符之间的联系都是通过简单的数学加法运算表示,不仅提高了检索速度,而且省去了链式结构中使用的大量指针,节省了存储空间。——《基于双数组Trie树算法的字典改进和实现》
双数组Trie树主要的优点就是相比链式结构Trie树大大降低了内存占用,是一种空间复杂度低的Trie树,其使用两个一维数组 BASE 和 CHECK 来表示整棵树。
DAT中有几个基本的概念
STATE : 状态,实际是BASE数组的下标;
CODE : 字符编码表;
BASE : 表示后继节点的基地址的数组;
CHECK : 表示前驱节点的地址的数组;
BASE 和 CHECK 构建的规则如下
BASE[s] + c = t
CHECK[t] = BASE[s]
举个🌰 , 如果字符h,加上字符e,可以组成前缀he。

则有BASE[h] + e = he,表示h和e的状态转移关系,另外CHECK[he] = h确保该状态转移的正确性。
三、构建双数组Tire树
这里以模式串 { he, hers, his, she} 为例,来讲解双数组trie的构建,其对应的Trie树结构如下图所示。
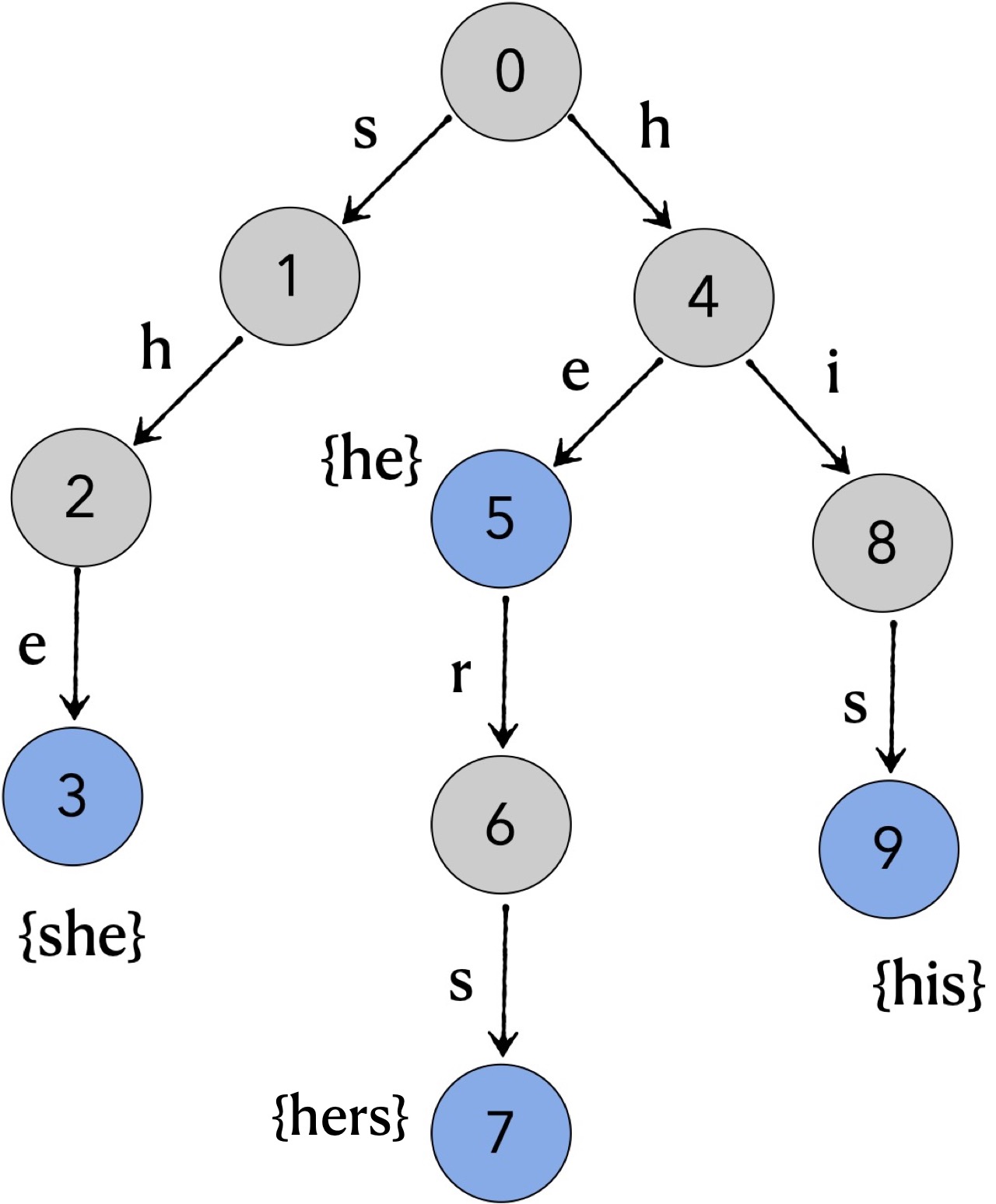
1. 构建CODE编码表

2. 构建BASE和CHECK状态表
假设当前状态为S,S的后继节点的字符为{A、B、C…},BASE[S]需满足
BASE[S] + CODE(A) = BASE[S] + CODE(B) = BASE[S] +CODE(C) = ... = 0
CHECK[BASE[S] + CODE(A)] = CHECK[BASE[S] + CODE(B)] = CHECK[...] = 0
确定了BASE[S]的值之后,需要将子节点位置的CHECK值设为S
CHECK[BASE[S] + CODE(A)] = CHECK[BASE[S] + CODE(B)] = ... = S
2.1 初始化Double Array
将根节点状态置为1,check置为0,将第一层结点h和s对应位置的值初始化为1,因为没有前缀,将CHECK设为-1(也可以是1)
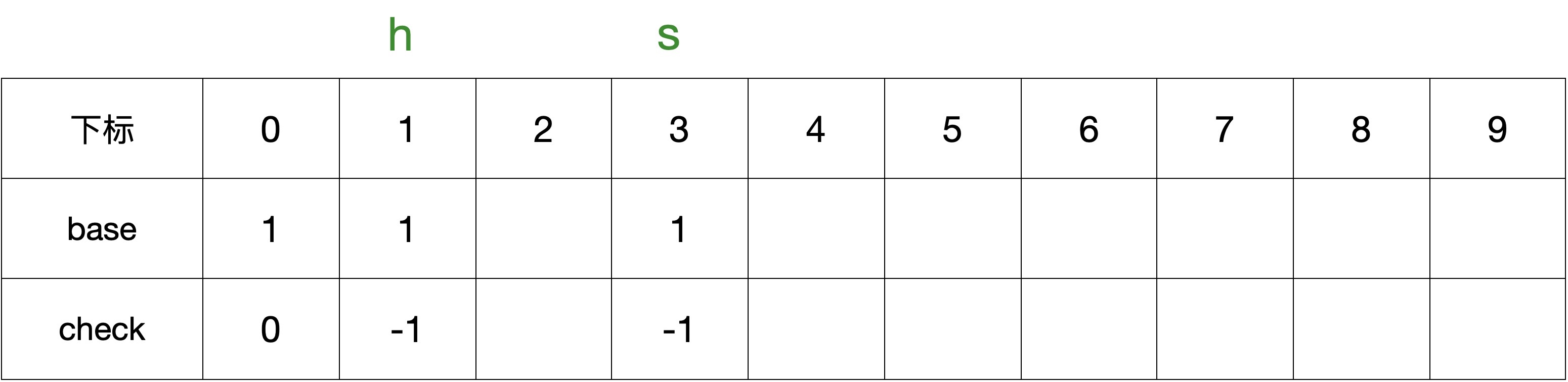
2.2 第一层节点的字符s
首先处理第一层节点的字符s,由于CODE(s) = 3,即确定 BASE[3]的值。
BASE[3]的后继子节点字符为h,CODE(h) = 1,可以得出其begin值为1,即 BASE[3] = 1。
同时状态转移需要满足:
CHECK[t] = BASE[s], 即 CHECK[2] = 3
赋值后的 BASE 和 CHECK 数组如下
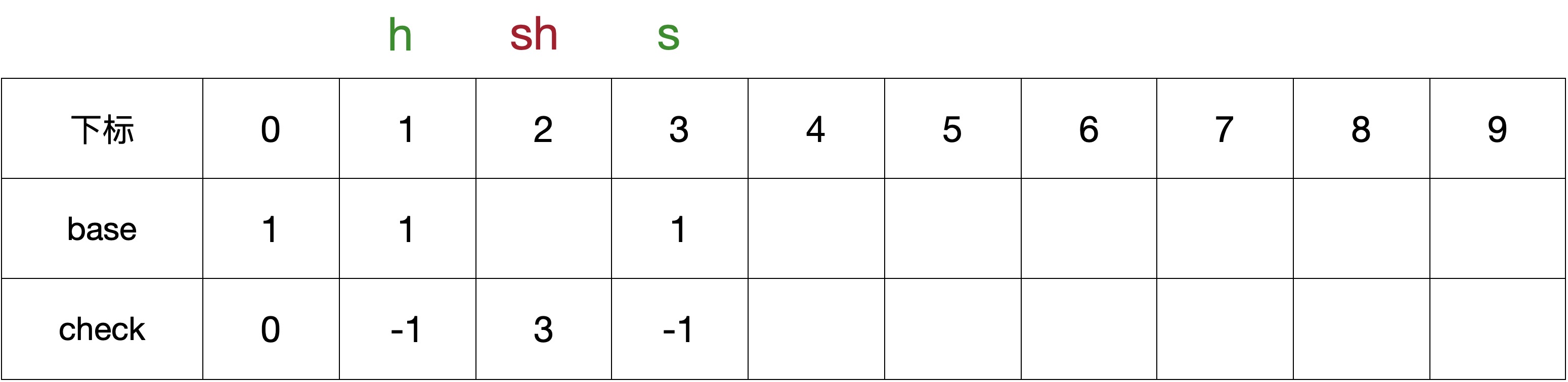
2.3 第一层节点的字符h
第一层节点的字符h,由于CODE(h) = 1,即确定 BASE[1]的值。
BASE[1]的后继子节点字符为e、i,CODE(e) = 2,CODE(i) = 4
- 当begin = 0的话,由于CHECK[2] != 0,所以不成立;
- 当begin = 1的话,由于BASE[3] != 0,所以不成立;
- 当begin = 2的话,
BASE[4] == BASE[6] == 0 && CHECK[4] == CHECK[6] == 0,则begin值可为2,即 BASE[1] = 2。
另外给子节点的CHECK进行赋值
CHECK[BASE[1] + CODE(e)] = CHECK[BASE[1] + CODE(i)] = 1
赋值后的 BASE 和 CHECK 数组如下
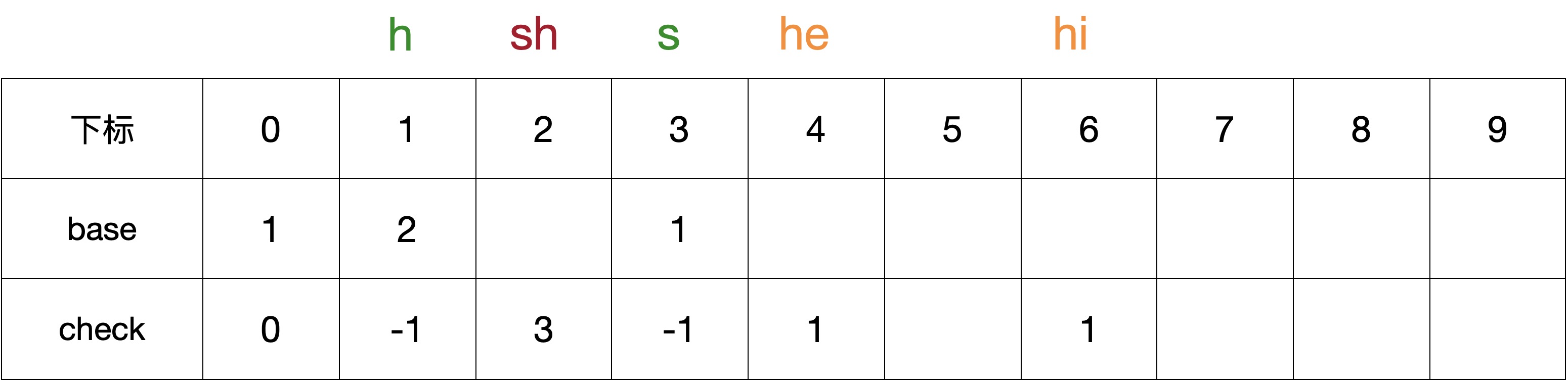
2.4 第二层节点的字符h
第二层节点的字符h对应的状态是BASE[2],只有一个子节点e,CODE(e) = 2;
- 当begin = 0,CHECK[2] != 0,不成立;
- 当begin = 1,BASE[3] != 0,不成立;
- 当begin = 2,CHECK[4] != 0,不成立;
- 当begin = 3,BASE[5] == 0 & CHECK[5] == 0,成立,则BASE[2] = 3,CHECK[5] = 2;
赋值后的 BASE 和 CHECK 数组如下
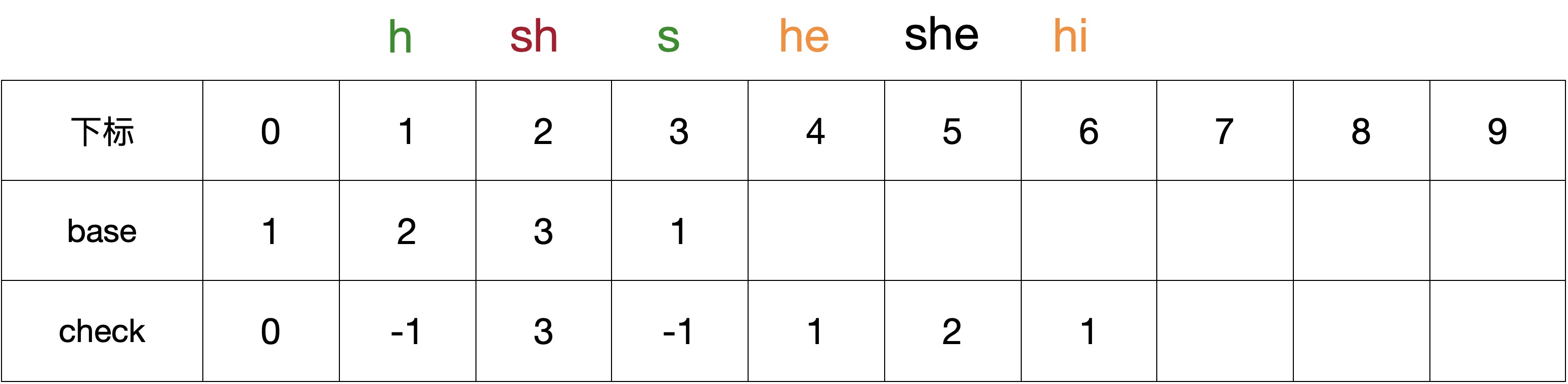
2.5 第二层节点的字符e
第二层节点的字符e对应的状态是BASE[4],只有一个子节点r,CODE® = 5;
- 当begin = 0,CHECK[2] != 0,不成立;
- 当begin = 1,BASE[3] != 0,不成立;
- 当begin = 2,BASE[7] == 0 & CHECK[7] == 0,成立,则BASE[4] = 2,CHECK[7] = 4;
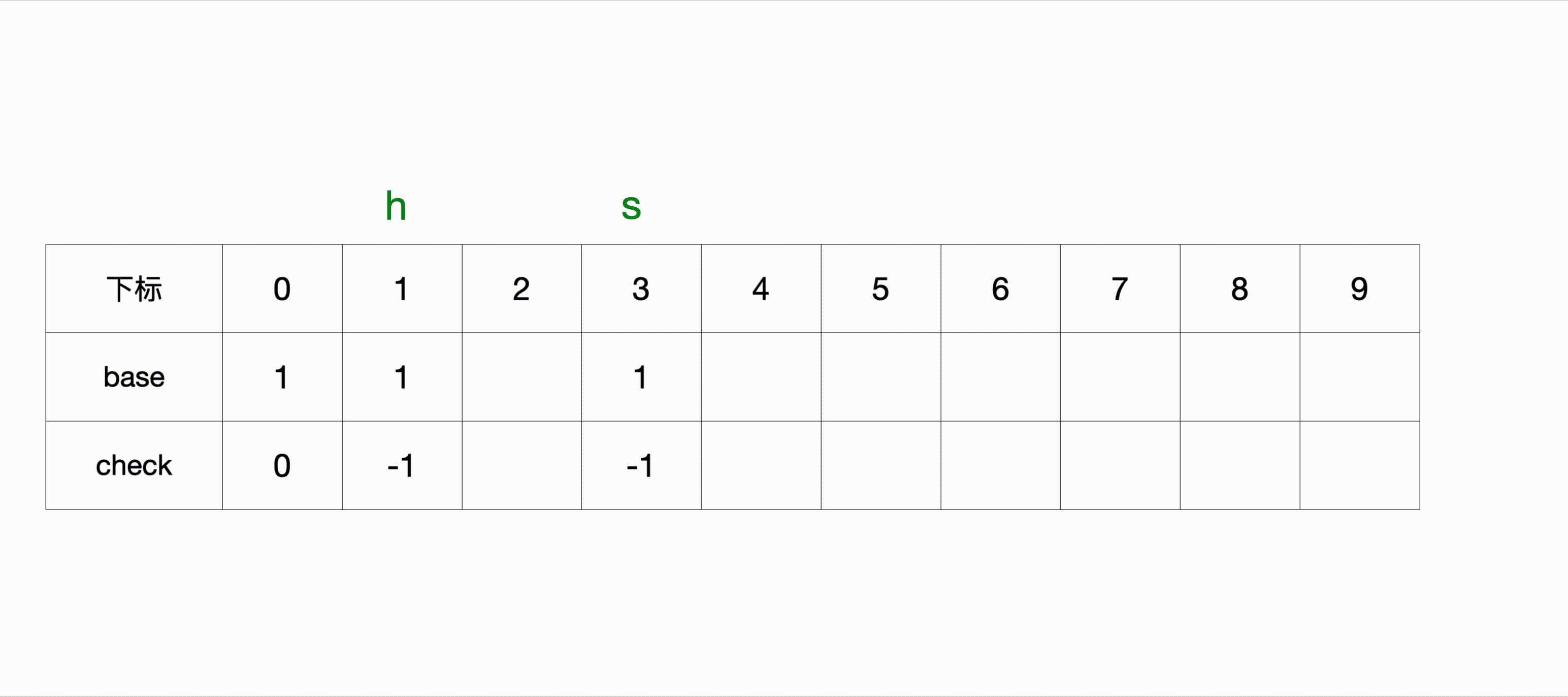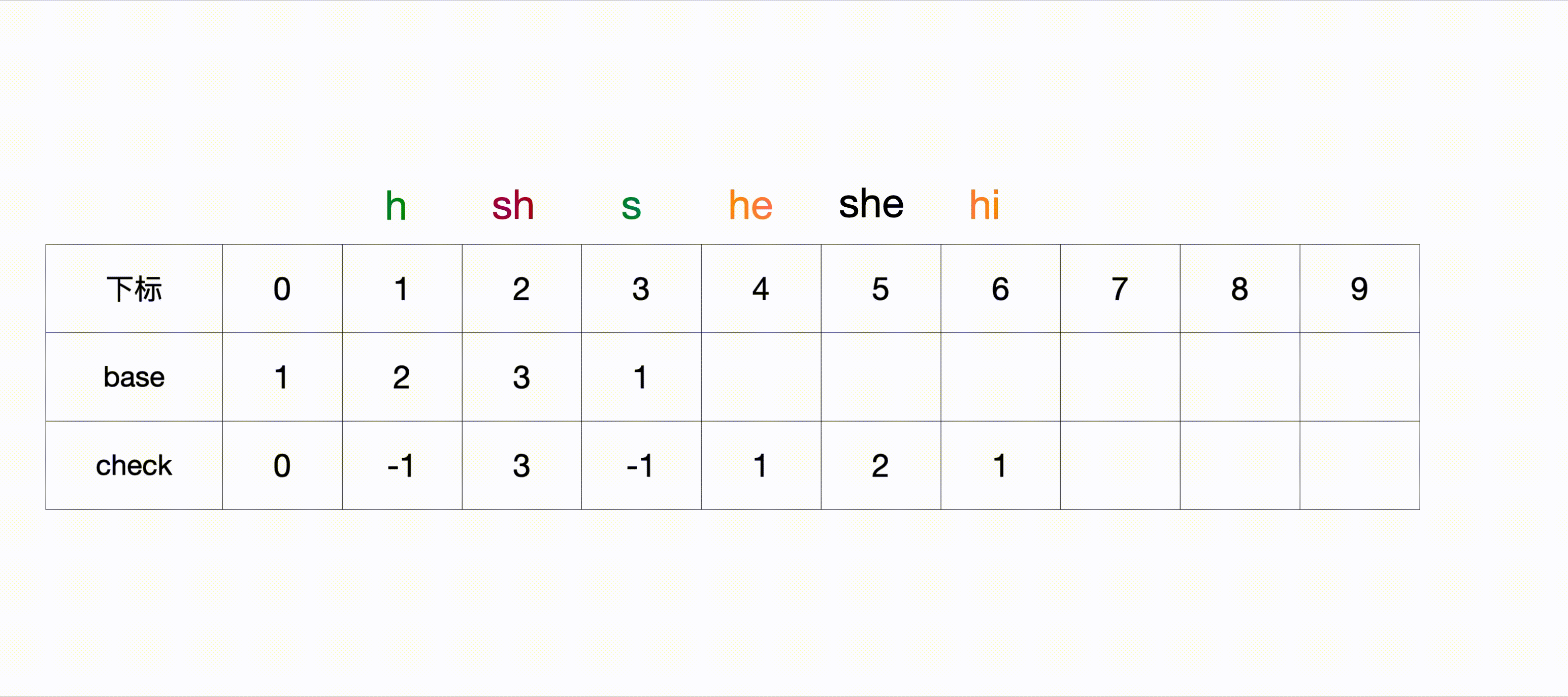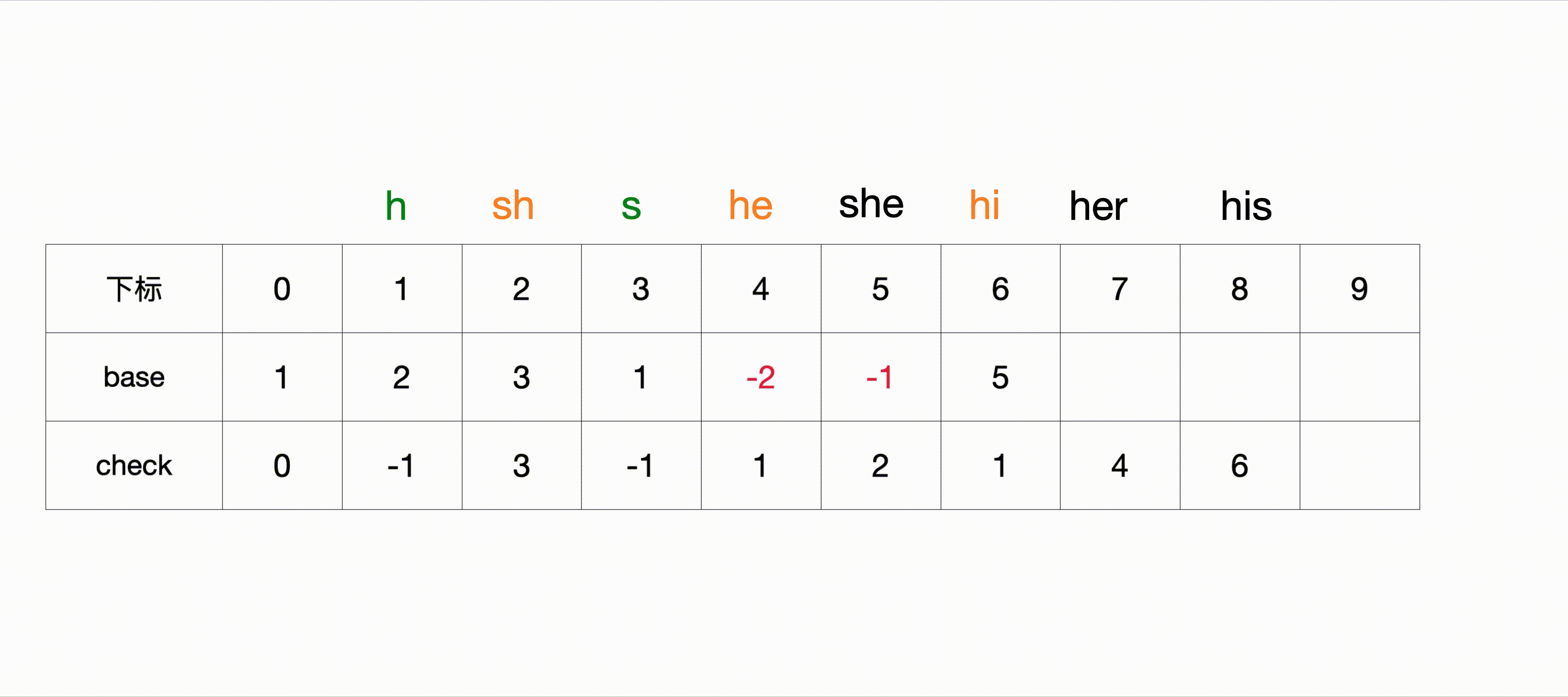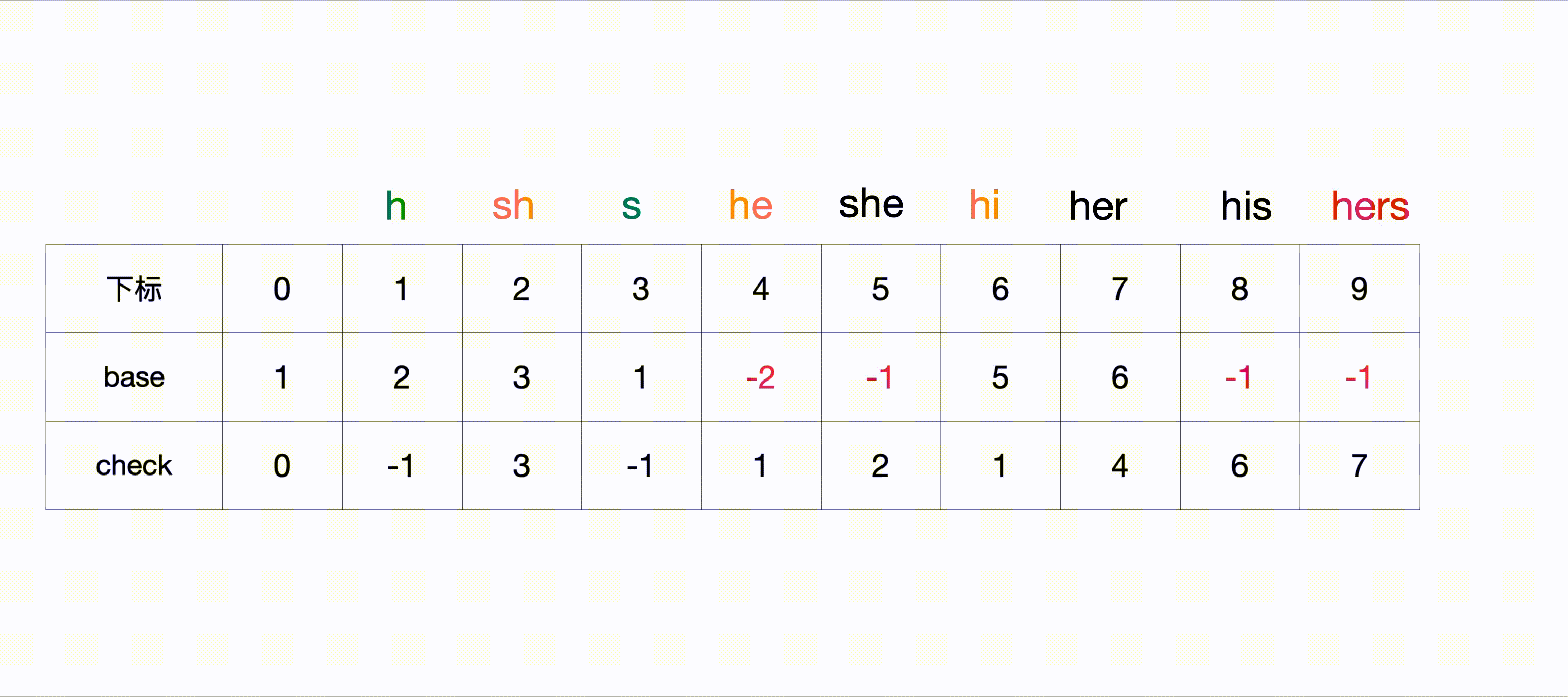
因为he为关键词,则将其base状态设置为负值,赋值后的 BASE 和 CHECK 数组如下
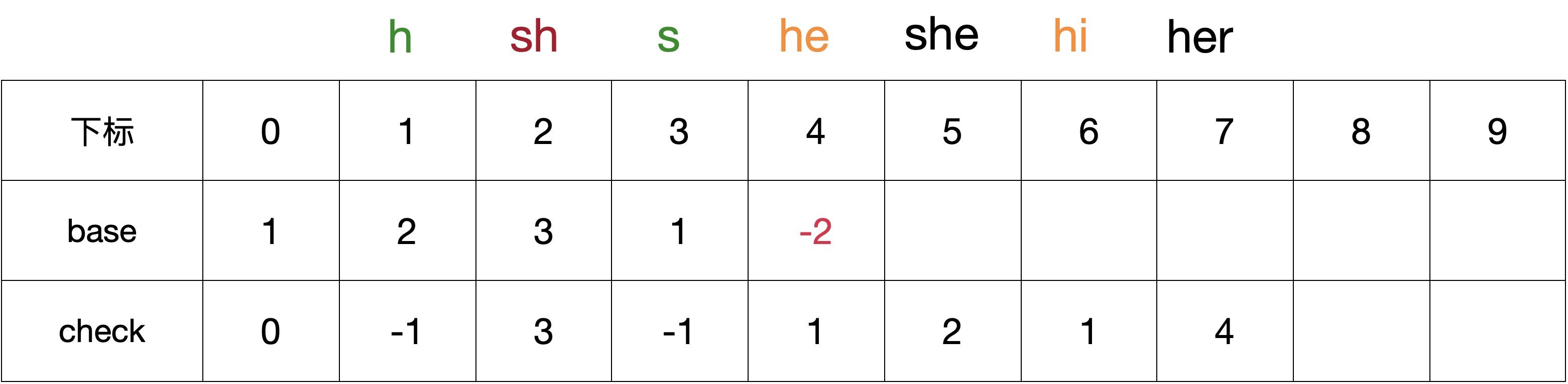
2.6 第二层节点的字符i
第二层节点的字符e对应的状态是BASE[6],只有一个子节点s,CODE(s) = 3;
根据上面的规则可得,begin = 5,则则BASE[6] = 5,CHECK[8] = 6;
赋值后的 BASE 和 CHECK 数组如下
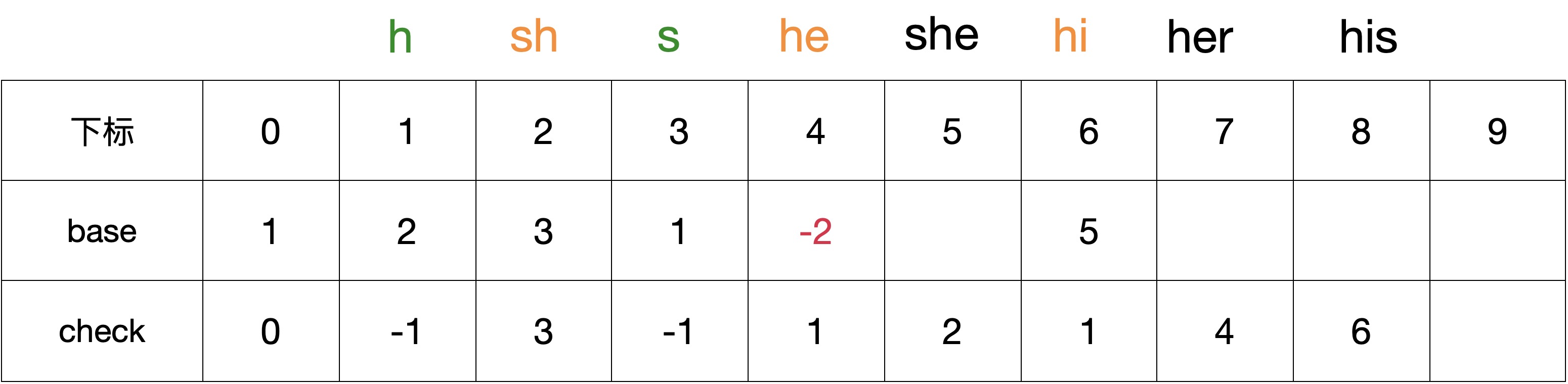
2.7 按规则初始化第三层和第四层节点
整个初始化的过程如下
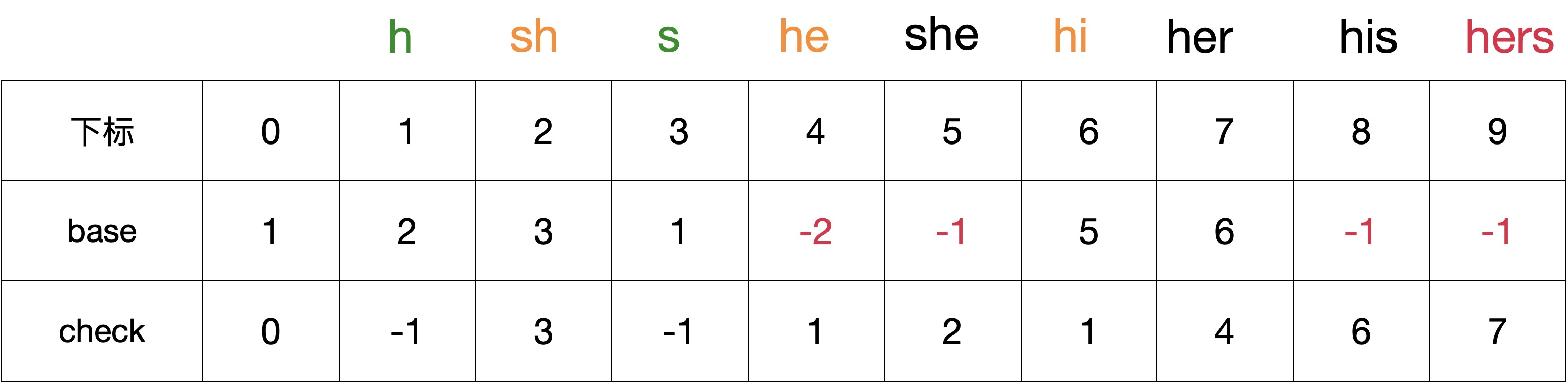
最终 BASE 和 CHECK 数组如下
四、构建适配数组
AC自动机是由Tire树配合适配指针构成,Trie树由双数组表示后,适配信息也由数组的方式来表示。
下图中的虚线是由指针形式表示的适配信息。
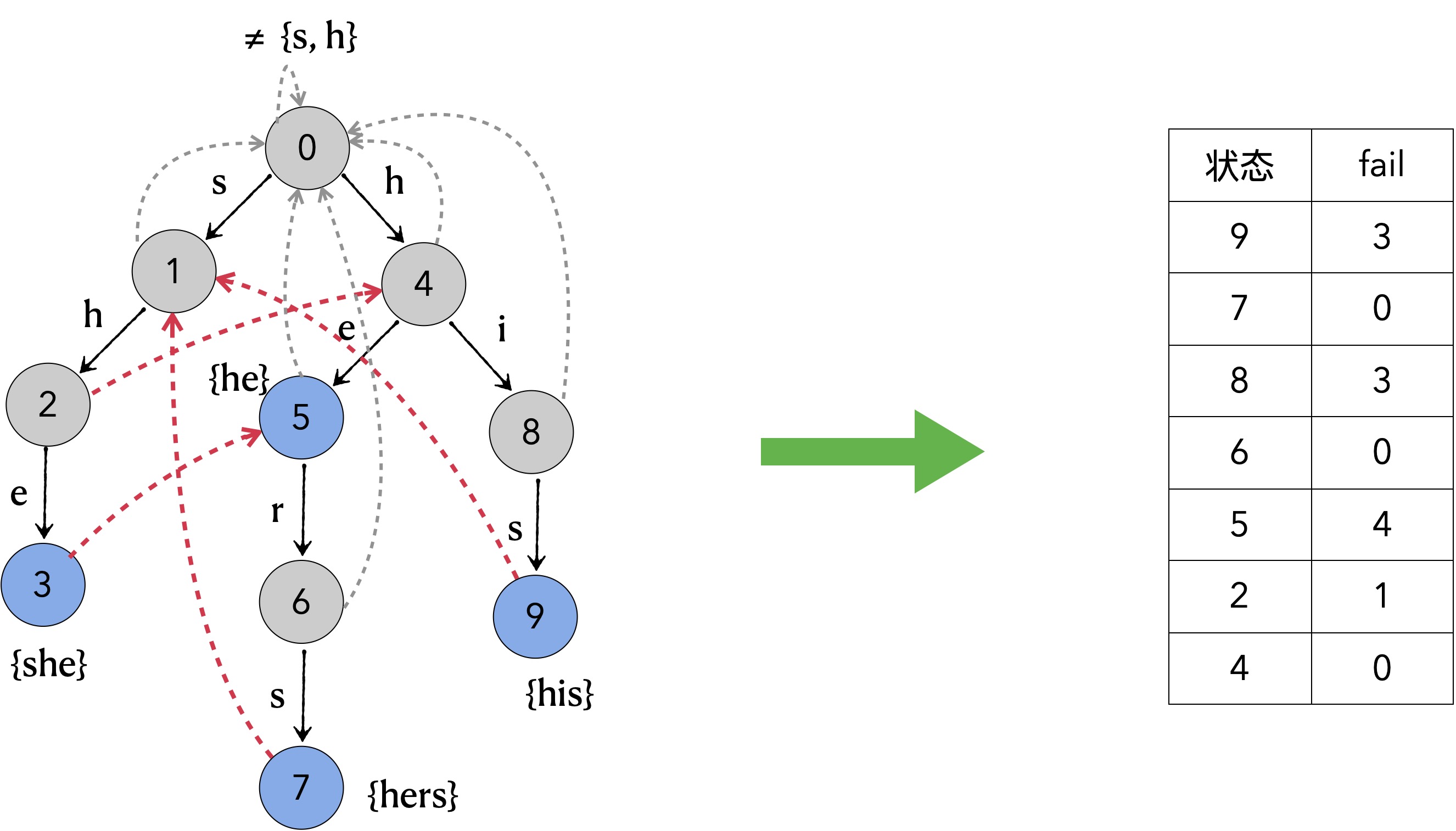
五、内存占用
测试过程中29W个关键词来构建出的基于双数组Trie树的AC自动机,占用内存超过60M。
其中
2110589长度的check 和 base数组(16M)
758618长度的<int, int> fail状态转移 map (5.7M)
29W个<int, string> 的状态到关键词的map(23M)
 内存还是很高,虽然内存还有优化的空间,但是也很难做出一个数量级的优化,那对于在内存受限的设备上,如何实现更性能高效,低内存占用的多模式匹配呢?
内存还是很高,虽然内存还有优化的空间,但是也很难做出一个数量级的优化,那对于在内存受限的设备上,如何实现更性能高效,低内存占用的多模式匹配呢?