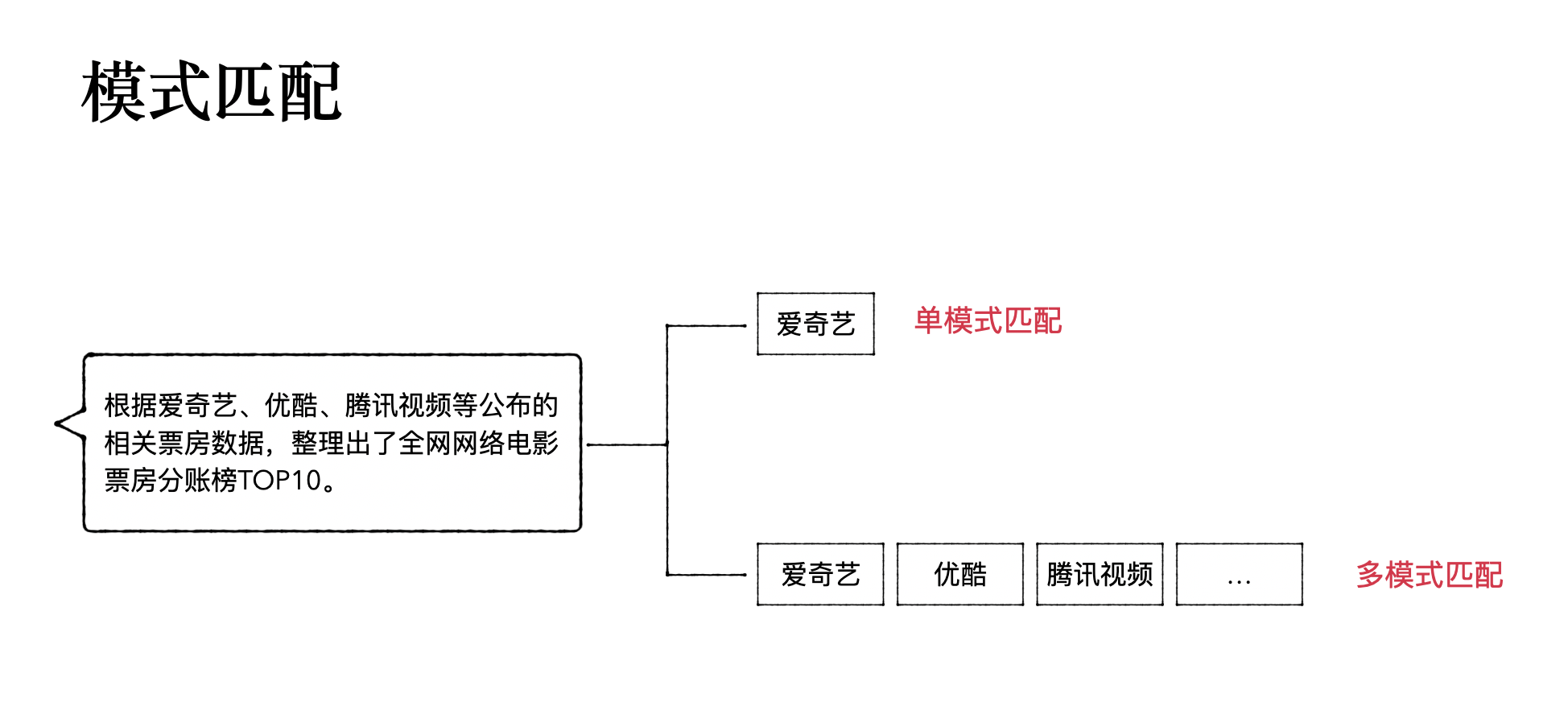
根据爱奇艺、优酷、腾讯视频等公布的相关票房数据,整理出了全网网络电影票房分账榜TOP10。
在文本中找出爱奇艺是否存在,这种单个关键词的查找,称为单模式匹配
在文本中找出爱奇艺,优酷,腾讯视频是否存在,这种多个关键词的查找,称为多模式匹配
多模匹配常用于关键字过滤、入侵检测、病毒检测、分词等场景;
常用的多模匹配算法有AC算法和WM算法,这里只介绍AC算法;
Aho-Corasick算法简称AC算法,通过将模式串预处理为确定有限状态自动机,扫描文本一遍就能结束。其复杂度为O(n),即与模式串的数量和长度无关。
AC自动机的构成
AC 自动机是 以 Trie 的结构为基础,结合 KMP 的思想 建立的,其由Tire树 + 失配信息所构成。
简单来讲建立AC自动机有两个步骤
- 基础的 Trie 结构:将所有的模式串构成一棵 Trie。
- KMP 的思想:对 Trie 树上所有的结点构造失配指针。
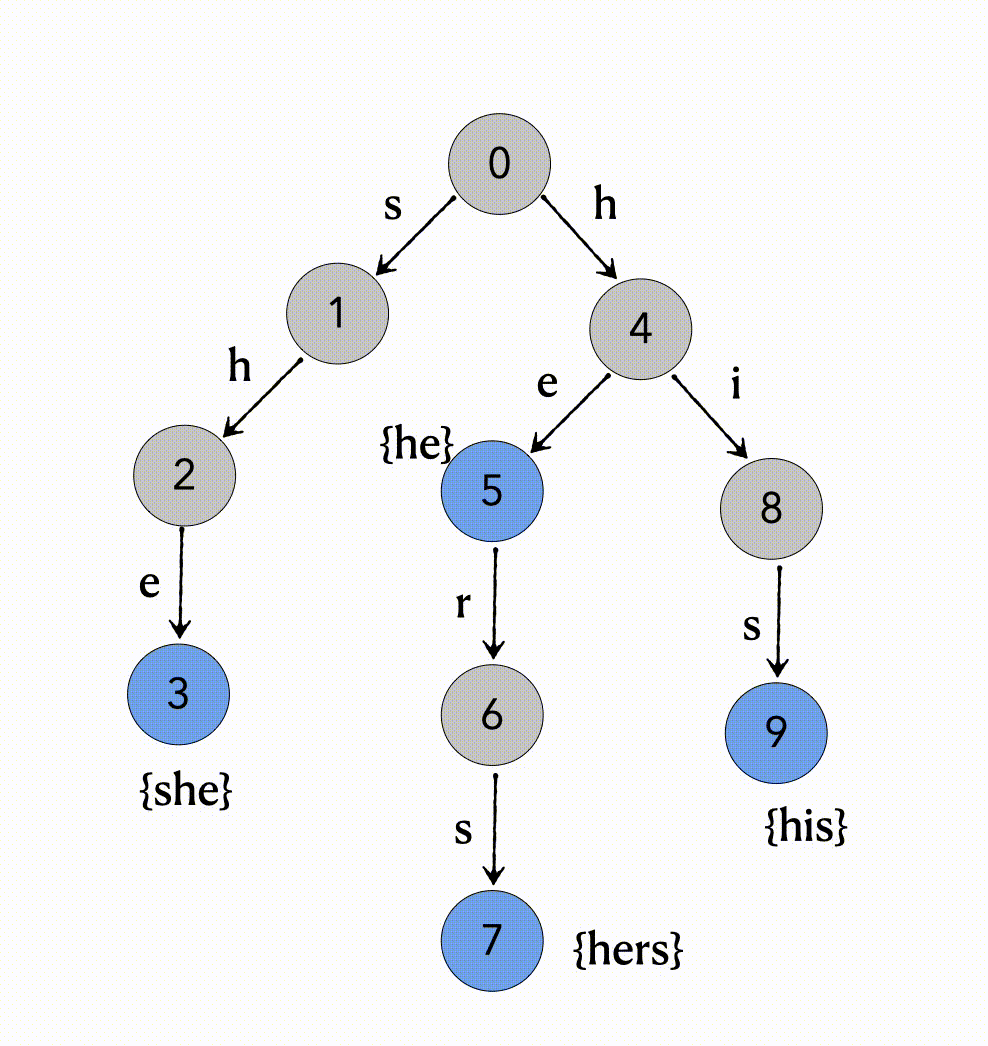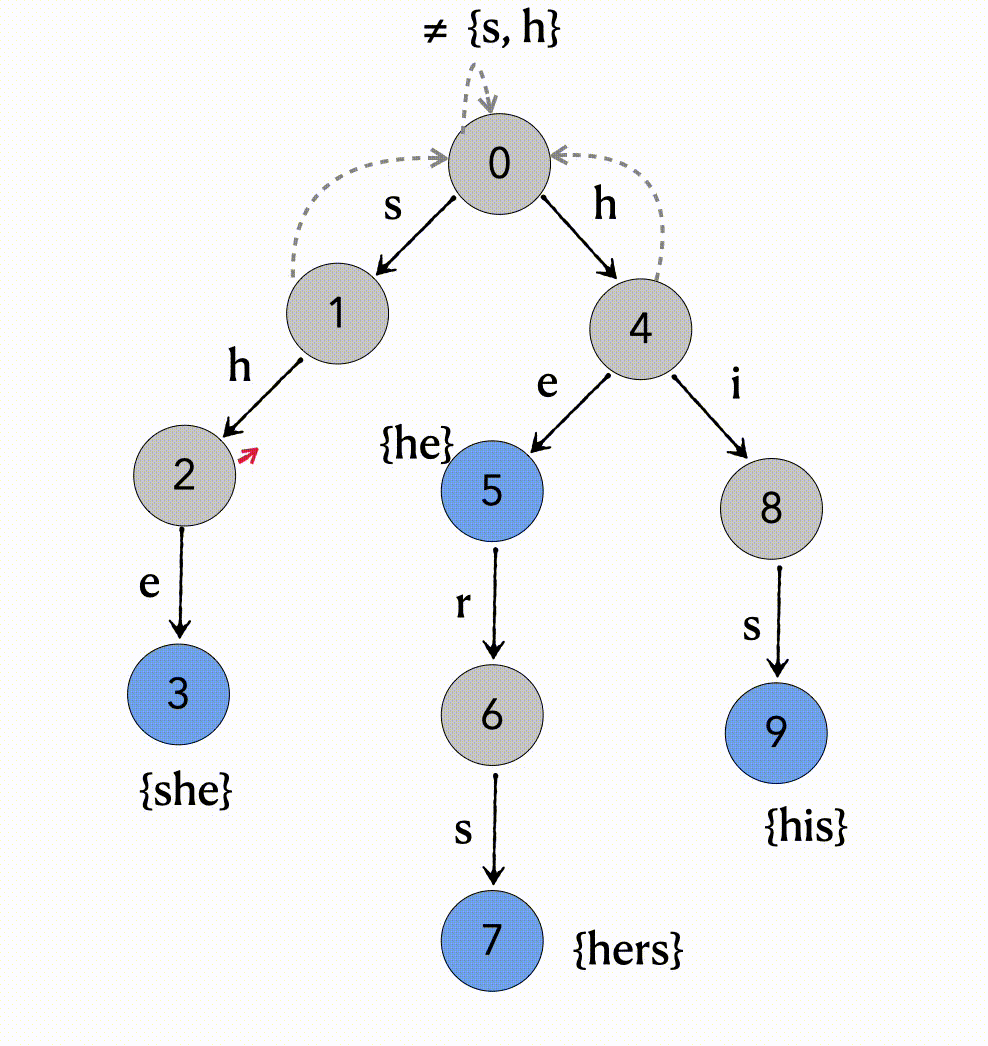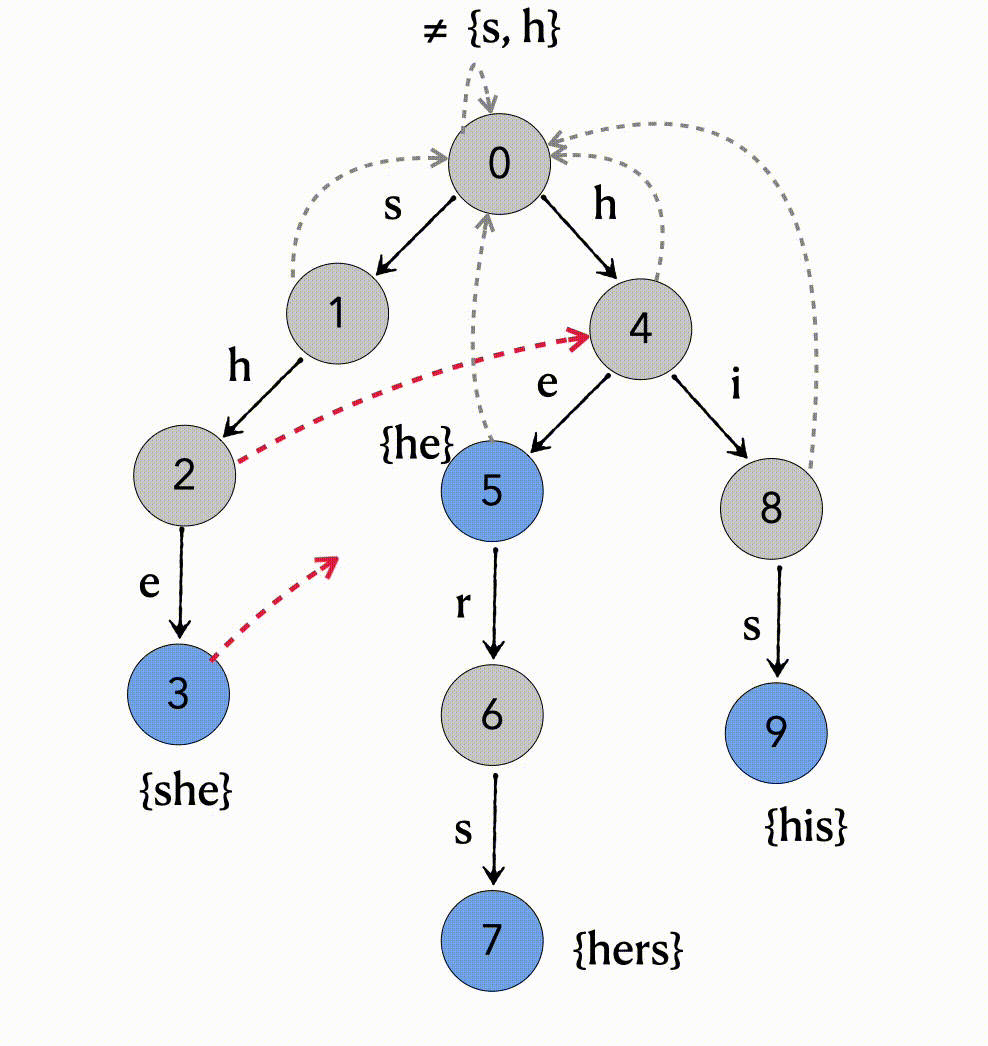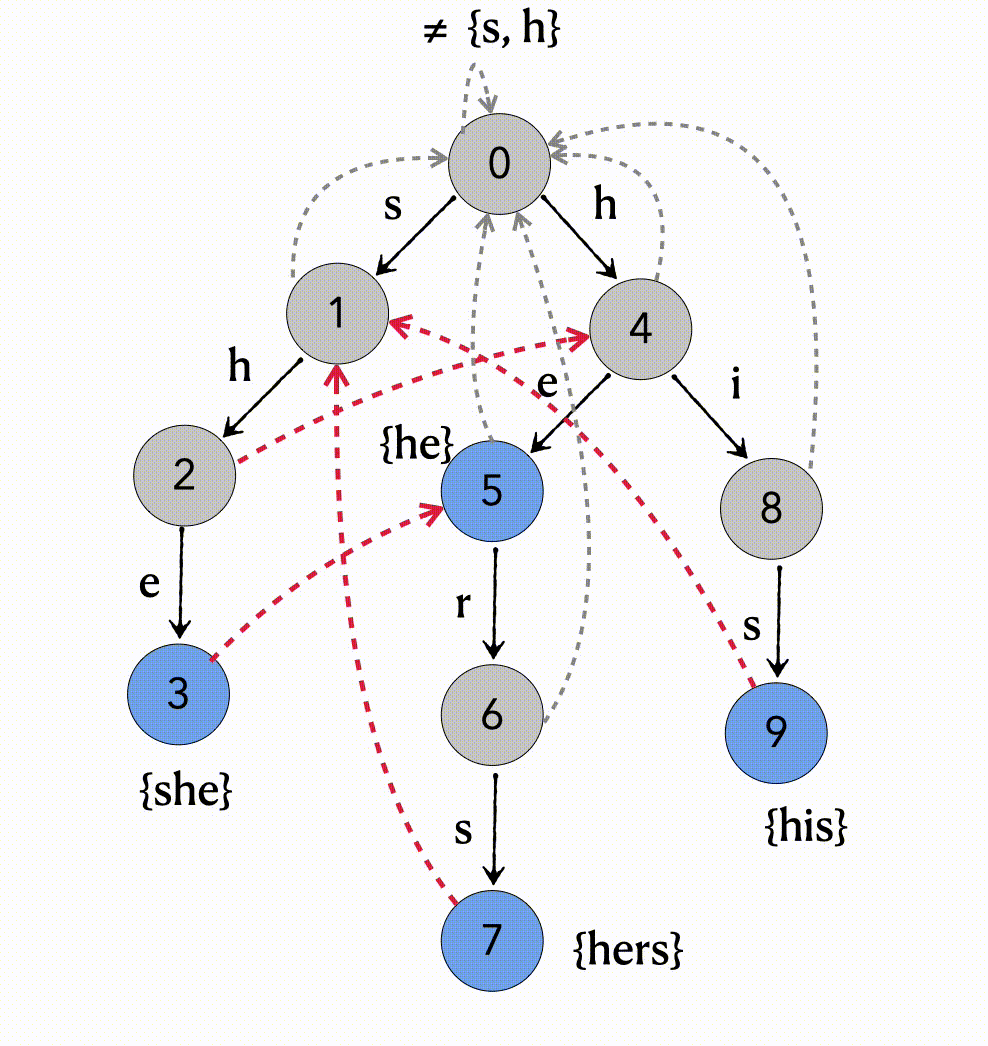
以{she, he, hers, his}为模式串,构建AC自动机。
Trie树的构建
将 {she, he, hers, his} 模式串建立Trie树,Trie树也成为前缀树或者字典树,形式化地说,于若干个模式串,将它们构建一棵Trie树后的所有状态的集合记作。
 这里需要仔细解释一下 Trie 的结点的含义,尽管这很小儿科,但在之后的理解中极其重要。
这里需要仔细解释一下 Trie 的结点的含义,尽管这很小儿科,但在之后的理解中极其重要。
Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态,Trie 的边就是状态的转移。
其中一个节点的表示代码如下
1 | struct TrieNode { |
失配指针
AC 自动机利用一个 fail 指针来辅助多模式串的匹配。
状态的fail指针指向另外一个状态,其中,且是的最长后缀。
fail指针与KMP的next数组相比区别如下
共同点:
都是在失配的时候用于跳转的信息;
不同点:
- next 指针求的是最长 Border(即最长的相同前后缀);
- fail指针则是所有模式串的前缀中匹配当前状态的最长后缀;
因为KMP是对一个模式串做匹配,而AC自动机则对应多个模式串做匹配。
对{she, he, hers, his} 模式串的Trie树构造失配指针过程如图
1、第一层根节点的fail指针指向自己,即输入≠ {s, h}的时候指向自己;
2、第二层的1、4的结点的fail指针指向根节点;
3、对于第三层的2号结点,先找到2号结点的父结点(1)的fail结点(root),遇到字符h可以转移到4号结点,则将2号结点的fail指针指向4号结点;
4、对于第三层的5号结点,先找到5号结点的父结点(4)的fail结点(root),遇到字符e(≠ {s, h})不能转移,将2号结点的fail指针指向root结点;
具体的init fail代码过程如下
1 | void init_fail() { |
匹配过程
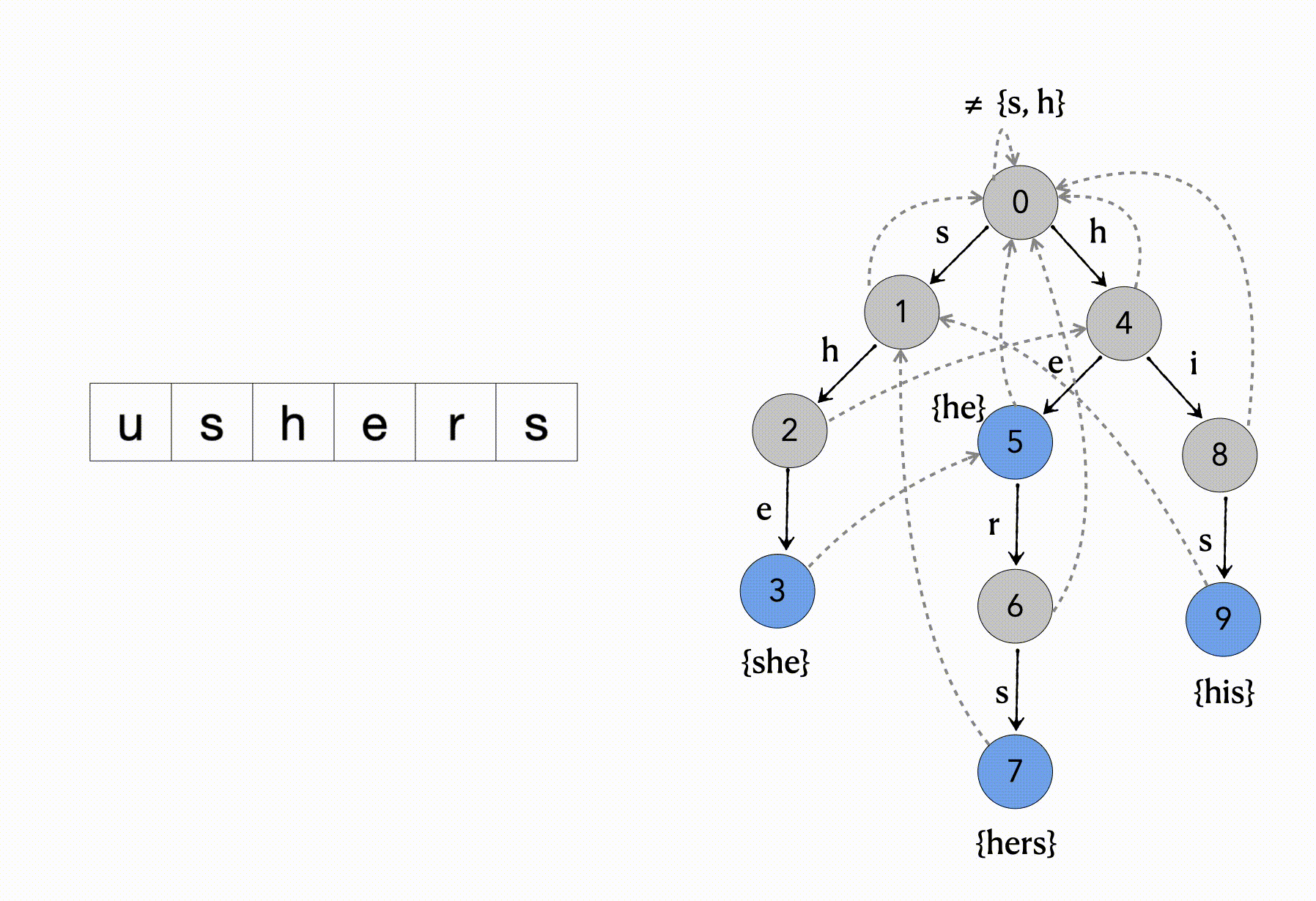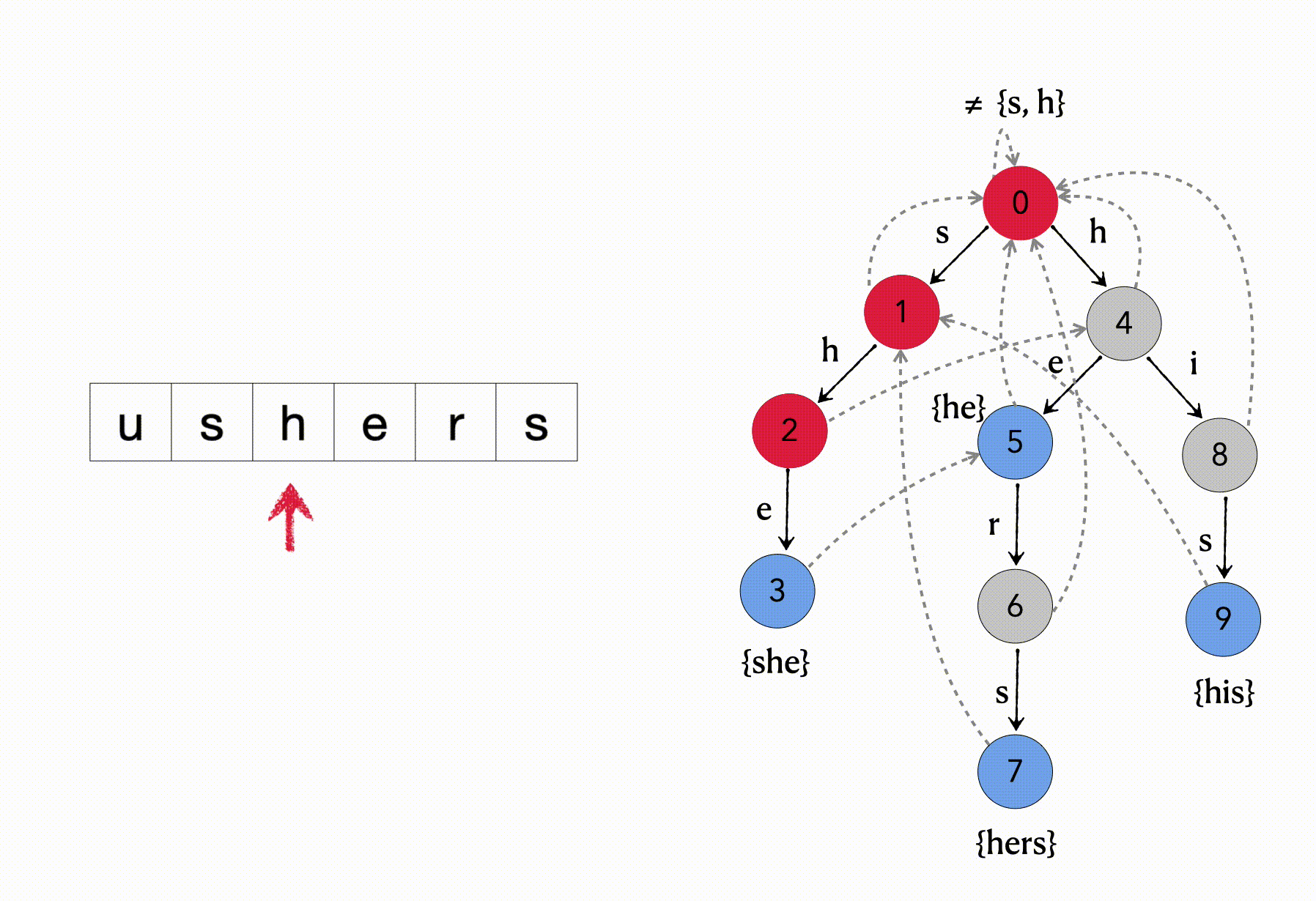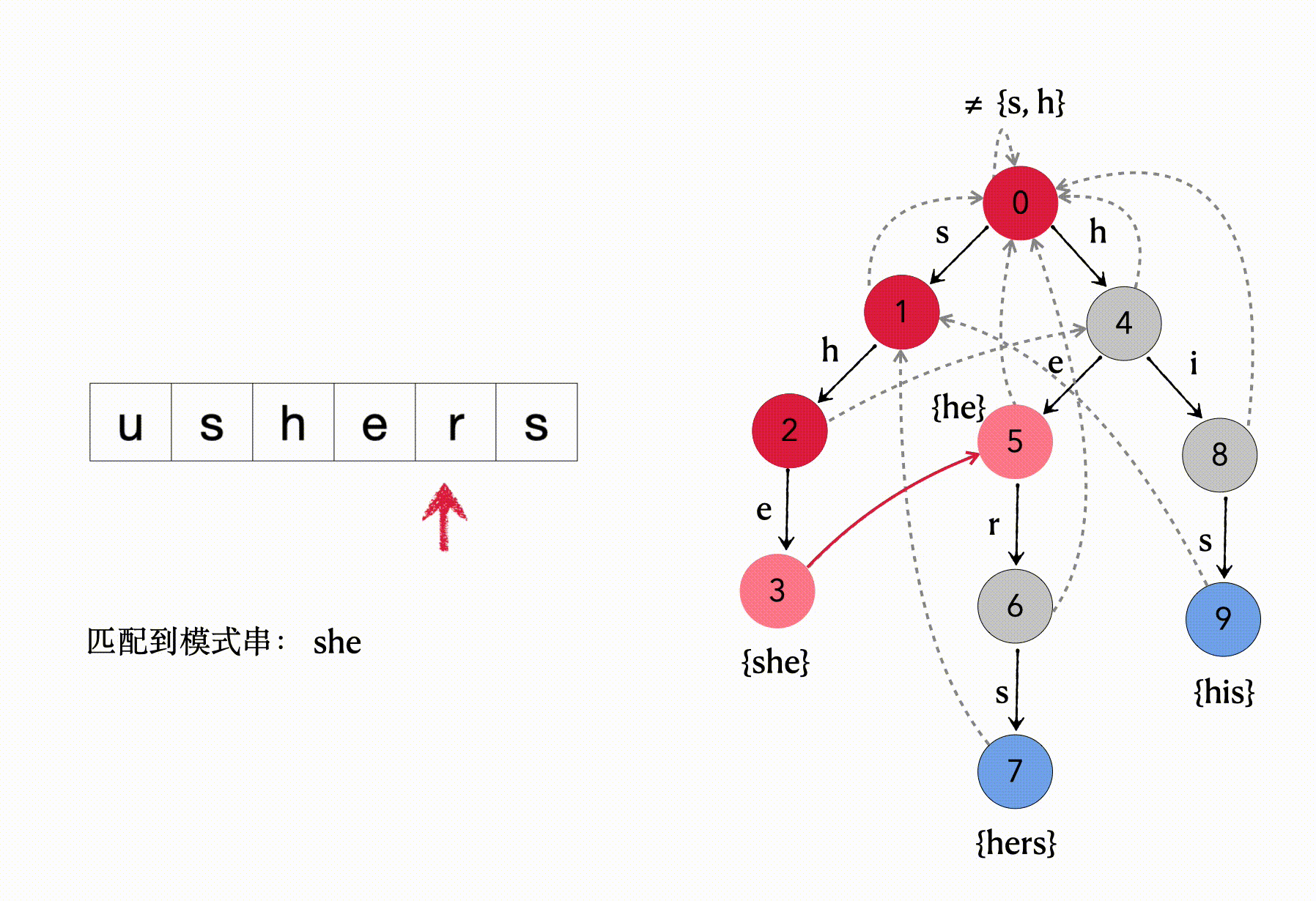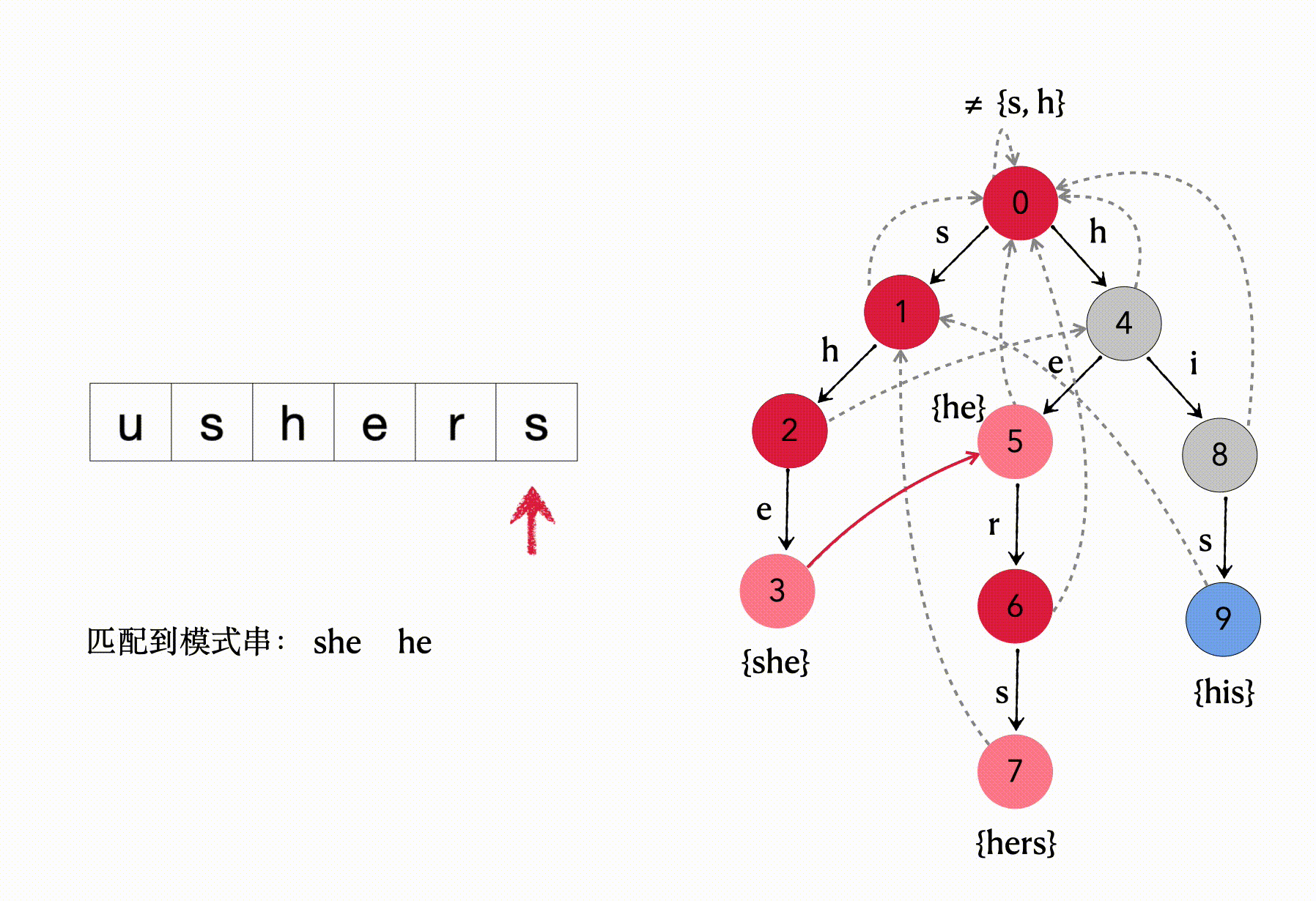 以模式串 {she, he, hers, his} ,文本“ushers”来简单的对匹配过程借助上图所示进行说明
以模式串 {she, he, hers, his} ,文本“ushers”来简单的对匹配过程借助上图所示进行说明
1、输入字符u ≠ {s, h},则root结点不进行状态转移;
2、输入字符s,从root结点转移到状态1结点;
3、输入字符h,从状态1转移到状态2;
4、输入字符e,从状态2转移到状态3,3号结点是关键字结束结点,则匹配到模式串she;
5、输入字符r,状态3无法正常转移,则根据fail指针转移到状态5,5号结点是关键字结束结点,则匹配到模式串he;
6、5号结点处理输入的r之后,转移到状态6结点;
7、输入字符s,从状态6转移到状态7,7号结点是关键字结束结点,则匹配到模式串hers;
8. 文本输入结束,最终匹配到she、he、hers
如果文本是“ushershis”,状态机在会怎样运行,会匹配到哪些模式串呢?
这个留给读者来思考吧。