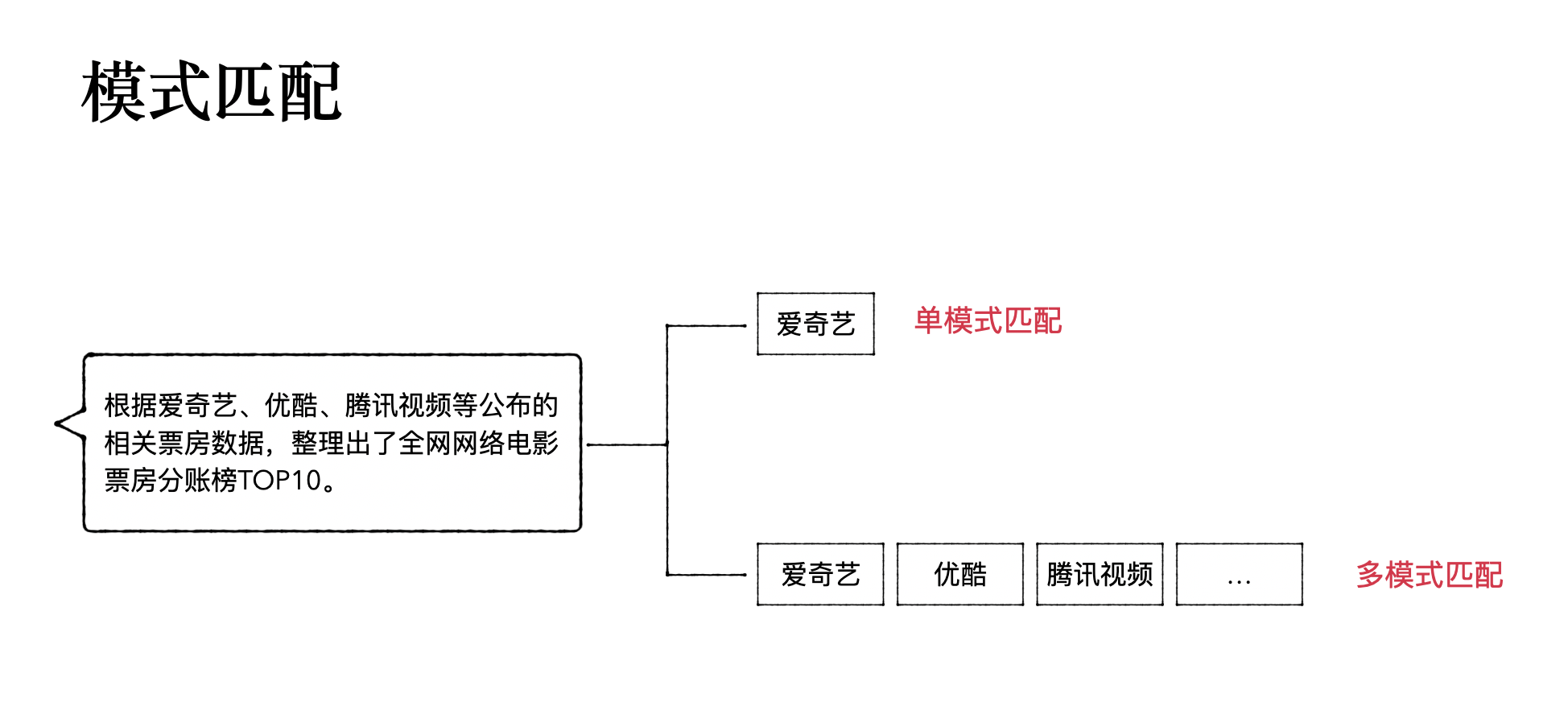
模式匹配分为单模式匹配和多模式匹配两种类型。
单模式匹配就是给定一串文本，查找单个子串是否在文本中；
多模式匹配就是给定一串文本，查找多个子串是否在文本中；
本文只介绍单模式匹配。
算法复杂度
假设给定的文本的长度为n，给定的子串的长度为m，判断子串是否在文本中。
暴力算法
算法复杂度为 O(n−m+1)∗m
KMP
算法复杂度为 O(n+m)
KMP算法
Knuth-Morris-Pratt算法（简称KMP）是最常用字符串匹配算法之一。
它以三个发明者命名，起头的那个K就是著名科学家Donald Knuth。
KMP的核心就是构建失配信息，构建失配信息的核心就是查找 前缀和后缀最长共有元素这里后面会进行介绍。
这里以文本“BBC ABCDAB ABCDABCDABDE”，子串“ABCDABD”的匹配过程为例来进行说明，
首先第一步B和A不匹配，直接后移一位；
第二步发现B和A也不匹配，再后移，直到匹配到第4位的A；
从第4位开始，ABCDAB都是和子串部分相匹配。
这个时候“D”字符无法继续匹配，按照一般的做法，我们会将子串后移一位，从下图的位置继续匹配。
但是KMP并不是这么做的，KMP会直接向后移动4位,然后将文本的“ ”和子串的“C”进行匹配，这样直接减少了很多不必要的匹配操作；
失配信息表
失配信息表是在匹配过程中出现失配情况的跳转依据，其核心思想就是
查找当前模式子串的前缀和后缀最长共有元素
首先，要了解两个概念：“前缀”和“后缀”。
“前缀”指除了最后一个字符以外，一个字符串的全部头部组合；
“后缀”指除了第一个字符以外，一个字符串的全部尾部组合。
ABCDABD 的失配信息表如下
| 失配字符 |
A |
B |
C |
D |
A |
B |
D |
| 部分匹配值 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
其构造的方式就是按照查找当前已经匹配部分的前缀和后缀最长共有元素,
1
2
3
4
5
6
7
| - "A"的前缀和后缀都为空集，共有元素的长度为0；
- "AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；
- "ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
- "ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
- "ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。
|
失配跳转
在上面匹配过程中，在出现“D”字符失配的时候，直接往后移动了4位，移动规则如下
后移位数 = 已匹配的字符数 - 对应的部分匹配值
即 后移位数 = 6(ABCDAB) - 2 = 4，进行跳转以后，使用"C"和当前文本位置的“ ”继续进行比较，这就是KMP算法匹配的跳转过程。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
void init_next(string pattern, int next[]) {
unsigned long len = pattern.length();
next[0] = 0;
for(int i = 1,k = 0; i < len; i++) {
while(k > 0 && pattern[k] != pattern[i]) {
k = next[k - 1];
}
if(pattern[k] == pattern[i]) {
k ++;
}
next[i] = k;
}
}
bool search(string content, string pattern) {
int next[pattern.length()];
init_next(pattern, next);
int i = 0;
while (i <= content.length() - pattern.length()) {
int j = 0;
for (; j < pattern.length(); j ++) {
if (pattern[j] == content[i + j]) {
continue;
}
int jump = j - next[j - 1];
i += MAX(jump, 1);;
break;
}
if (j == pattern.length()) {
return true;
}
}
return false;
}
int main(int argc, const char * argv[]) {
bool exist = search("ABCDABCDABDE", "ABCDABD");
printf("kmp search exist:%u\n", exist);
return 0;
}
|
点击查看源码
参考
http://www.ruanyifeng.com/blog/2013/05/Knuth–Morris–Pratt_algorithm.html